Qué son las combinaciones
Cuando hablamos de combinaciones en poker nos referimos, valga la redundancia, a las distintas combinaciones de cartas que los jugadores de una partida pueden formar para ganar una mano. Por ejemplo, en una modalidad como el texas hold’em, los jugadores deben utilizar sus dos cartas tapadas para combinarlas con las cartas comunitarias y formar la combinación ganadora.

Es muy importante para los jugadores conocer cuáles son los valores y combinaciones en poker, ya que en eso debe basarse su estrategia a la hora de decidir si comprometerse o no con una mano. Para tomar la decisión correcta, primero debemos conocer cuánto vale nuestra combinación de cartas y cuánto creemos que vale la de nuestro rival.
Muchas salas de poker online, como PokerStars, Winamax o GGPoker, indican a los jugadores la combinación que van formando en cada momento de la mano, para que no tengan que gastar tiempo calculando sus combinaciones y puedan concentrarse simplemente en ver si son mejores que las de su rival.
Aquí puedes echarles un vistazo:
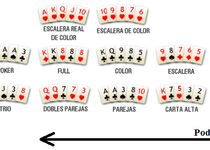
Todas las combinaciones
En una mano de poker puede conseguirse la victoria de dos maneras: haciendo foldear a todos tus oponentes o llegando al showdown con la mejor combinación de cartas. Para poder hacer esto, es necesario conocer todas las combinaciones del poker y sus respectivos valores.
A continuación, presentamos todas las combinaciones del poker, ordenadas desde la más débil hasta la más poderosa:
Carta alta
Muchas veces, lamentablemente, las cartas tapadas que recibes en tu mano no logran conectar con ninguna del board. Cuando eso ocurre, lo que se hace es comparar tus cartas de mayor a menor contra las de tu rival. Un as es la carta más alta que se puede tener en caso de que los jugadores no hayan logrado conectar una combinación.

En esta imagen, el jugador con el as se impone porque su carta es más alta que el rey de su rival. En este tipo de casos, se suele decir que el ganador lleva “as-high”, mientras que la mano del perdedor suele nombrarse como “rey-high”. En el caso de que ambos jugadores tengan la misma carta más alta, se compara la segunda carta más alta y así sucesivamente.
Par
Un par se consigue al conectar dos cartas del mismo valor. Esto puede lograrse conectando una carta de tu mano con una del board, así como también recibiendo directamente dos cartas tapadas iguales, lo que se conoce como un par en mano. Otra manera de formar un par es que se hayan repartido dos cartas de un mismo valor entre las comunitarias.

Doble par
Tal como su nombre lo indica, esta combinación se obtiene al conectar dos cartas de un mismo valor y otras dos cartas de otro mismo valor. Esto puede lograrse al conectar tus dos cartas tapadas con dos del board o teniendo un par en mano y que salga otro en las comunitarias.

Trío
El trío se conforma con tres cartas de un mismo valor, pero esto puede lograrse de dos formas distintas.
Por un lado, tenemos lo que se conoce comúnmente como “pierna”, la cual se forma al conectar una carta de nuestra mano con dos cartas comunitarias del mismo valor.

Por otro lado, existe lo que se conoce como “set”, y el mismo se forma al conectar un par en mano con una carta comunitaria del mismo valor. El set es una combinación en poker bastante fuerte, que suele tomar por sorpresa a los oponentes.

Existe un 11.8% de probabilidades de conectar un set en el flop
Escalera
Esta combinación se forma con cinco cartas consecutivas de cualquier palo. Puede lograrse utilizando las dos cartas de tu mano, así como una o ninguna. Una particularidad de la escalera es que en ella el as puede ser una carta, tanto alta como baja. La escalera más baja posible empieza con el as y la escalera más alta termina con el as.

Color
Para formar un color solo necesitamos cinco cartas de un mismo palo, sin importar que estén ordenadas. Se puede formar combinando tus dos cartas tapadas de un mismo palo con tres comunitarias o también combinando una carta de tu mano con cuatro comunitarias del mismo palo. Otra forma en la que se puede dar un color es que las cinco cartas comunitarias sean del mismo palo. En caso de que más de un jugador tenga color, gana quien tenga el color más alto y el color al as es el más alto que se puede tener.

Full House
En simples palabras, un full house es una combinación entre un trío y una pareja, ya que se forma con tres cartas de un valor y dos de otro. Puede conformarse de las siguientes maneras:
Con un par en mano que conecta con una tercera carta de su valor y otras dos de otro valor.
Con un par en mano que conecta con tres cartas de otro mismo valor en el board.
Con dos cartas distintas que conectan con tres cartas del board de esos valores.

Por ejemplo, en esta ilustración, el jugador ganador ha formado un full house con un par en mano que conectó un tercer diez y dos tres.
Poker
En español se le llama poker a la combinación de cuatro cartas de un mismo valor. Por ejemplo, si un jugador tiene dos ases en su mano y en las comunitarias se muestran dos ases más, tiene poker. También puede pasar que en el board salgan tres cartas del mismo valor que una de tu mano o que directamente salgan cuatro cartas comunitarias iguales.

Escalera de color
Habíamos visto que en el color no hacía falta que las cartas de un mismo palo estuvieran ordenadas. Pues bien, en la escalera de color ese es un requisito primordial, ya que la misma consiste justamente en cinco cartas consecutivas de un mismo palo. Es muy difícil ganarle a esta combinación, ya que solo puede lograrse con un escalera de color más alta.

Escalera Real
La escalera real sería algo así como la escalera de color más alta que puede haber. Se conforma con una secuencia del diez al as, con el requisito de que todas las cartas deben ser del mismo palo. Nada le gana a esta combinación.

Si tienes la increíble fortuna de conectar una escalera real, de lo único que debes preocuparte es de sacarle el valor adecuado, ya que, si bien es invencible, puede llegar a ser todo un desafío hacer que tus oponentes paguen tus apuestas si no tienen al menos una mano decente.
Si todavía tienes alguna duda para empezar a dar tus primeros pasos en el mundo del poker, no dudes en contactar con nuestro equipo de soporte.
- Mayor rakeback y bonos personales
- Ayuda con depósitos y retiros
- Acceso a aplicaciones móviles
- Resolvemos problemas con cuentas
- Soporte técnico
- Preguntas acerca del sitio y el foro
Qué es un proyecto
No siempre vamos a encontrarnos con combinaciones formadas desde el comienzo de la mano. Muchas veces, lo que tendremos serán proyectos, los cuales son manos que podrían llegar a mejorar y formar alguna combinación en caso de conectar con alguna carta comunitaria específica en el futuro. Las cartas que nos ayudarían a completar nuestros proyectos son llamadas “outs”. Saber cuándo aferrarse a un proyecto y cuándo dejarlo ir es lo que separa a los principiantes de los jugadores ganadores.
Proyecto a color
Si necesitas una carta para completar tu combinación de cinco naipes del mismo palo, tienes un proyecto a color. En caso de que tan solo tienes tres cartas de un palo y necesites que salgan dos más, entonces tienes un proyecto a color “backdoor”.

| En el flop | En el turn | En el river | |
| Probabilidades de concretar un color con dos cartas tapadas del mismo palo | 0.8% | 19.1% | 19.6% |
Proyecto de escalera
Tienes un proyecto de escalera cuando puedes llegar a formar una con la ayuda de una carta comunitaria. Si tienes cuatro cartas consecutivas y necesitas que salga una carta, ya sea la que empiece o la que termine la escalera, tienes una escalera “a dos puntas”. Si, en cambio, la carta que falta para tu escalera va en medio de la secuencia, tienes un proyecto de escalera “al hueco” o “gutshot”. Al igual que con el color, si te faltan dos cartas para completar tu combinación, entonces tienes un proyecto “backdoor”.

| En el flop | En el turn | En el river | |
| Probabilidades de completar una escalera a dos puntas | 1.3% | 17% | 17.4% |
| Probabilidades de completar una escalera gutshot | 1.3% | 8.5% | 8.7% |
El kicker y los desempates
En el poker se utiliza el kicker como la carta suelta más alta que acompaña a las combinaciones. Por ejemplo, imaginemos una situación en la que dos jugadores lograron formar exactamente el mismo par. ¿Cómo sabemos quién ganó? Comparamos sus cartas más altas por fuera del par, ese es el kicker. Usualmente, se utiliza para desempatar en casos de par o doble par. Por lo general, los jugadores buscan acompañar sus juegos con buenos kickers, por eso son consideradas fuertes las manos como AK, ya que en caso de conectar cualquiera de las dos, no solo se obtiene el par más alto, sino también el kicker más alto.
Kicker en el par
Cuando dos jugadores tienen el mismo par, se comparan sus cartas más altas por fuera del par, como se ve en la imagen a continuación.

En esta ilustración, el jugador con el par de ases y el kicker rey le gana al jugador con par de ases y kicker reina.
Kicker en el trío
Si dos jugadores forman el mismo trío, se utilizan sus cartas más altas por fuera del mismo para desempatar, como se ve en la imagen a continuación.

Kicker en poker
En el extraño caso de que haya cuatro cartas de un mismo valor sobre las comunitarias, gana el jugador que desempate con la quinta carta más alta.

Cuando no hay kicker
Hay combinaciones en poker que no llevan kicker, ya que de por sí son de cinco cartas, como la escalera y el color.
En el caso de las escaleras, simplemente se compara cuál de los jugadores ha logrado formar la escalera más alta, y si ambos tienen la misma se declara un empate.

Cuando dos jugadores tienen color, siempre uno de los dos tendrá uno más alto que el otro, a menos que las cinco cartas del mismo palo hayan sido repartidas en el board.

Esperamos que tras la lectura de este artículo tengas una mejor idea de cómo funcionan las combinaciones en poker. No dudes en volver a revisar las reglas del poker en caso de que te hayas quedado con alguna duda al respecto.